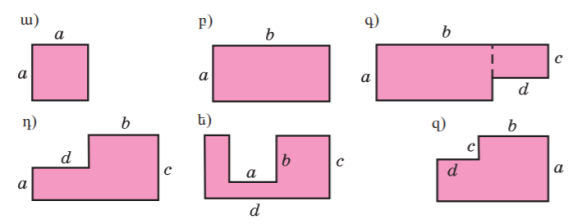Рубрика: Մաթեմատիկա

1. Տառային արտահայտության տեսքով գրի՛ առեք գործողությունների
հետևյալ հաջորդականությունը.
ա) a թիվը բազմապատկել 4-ով և արտադրյալին գումարել 6,
a x 4+ 6
բ) y թվից հանել 11 և տարբերությանը գումարել z թիվը,
y — 11+ z
գ) 10-ը բաժանել a թվին և քանորդին գումարել 15-ի և b թվի արտադրյալը,
(10 : a)+(15x b)
դ) m թվին գումարել 5 և գումարը բազմապատկել n թվով:
m+ 5 x n

2. Դիցուք, տրված է a թիվy: Կազմեք տառային արտահայտություն և գրի՛ առեք.
ա) այդ թվի կրկնապատիկը,
ax2=2a
բ) այդ թվի կեսը,
a:2=a\2
գ) այդ թվի երկու երրորդը,
a:3×2=ax2\3
դ) այդ թվից հինգով մեծ թիվը,
a+5
ե) այդ թվից 10-ով փոքր թիվը:
3. Կատարե՛ք հաշվումները, եթե a = 3.
ա) 3 ⋅ a + 386, գ) (17 – a) ⋅ 3, ե) (78 ։ a + 99 ։ a) ⋅ 5,
բ) 27 ։ a + 96 ։ a, դ) (6 ⋅ a + 3) ⋅ a, զ) a ⋅ 2 + a ⋅ 3 + a ⋅ 4։

4. Գտե՛ք տառային արտահայտության արժեքը, եթե a = 7, b = 5.
ա) 3 ⋅ a + 5 ⋅ b=46, գ) (a – b) ⋅ 4 + a ⋅ b=43, ե) (a – 7) ⋅ 8 + (b – 5) ⋅ 4=24,
բ) 10 ⋅ (a + b) ։ 3=, դ) 95 ։ b + 49 ։ a, զ) (a – 7) ⋅ (b – 5)։5=1. Գրե՛ք մեկի հատկությունները՝ օգտագործելով տառային նշանակում­ներ։

Լրացուցիչ առաջադրանքներ

6. Տրված պատկերի S մակերեսը հաշվելու համար կազմեք տառային
արտահայտություն.

Թվերից, թվաբանական գործողություններից և փակագծերից կազմված իմաստալից արտահայտություններն անվանում ենք թվային արտահայտություններ։

Օրինակ՝  25* (106 — 196:4): 

Կարող ենք հաշվել յուրաքանչյուր թվային արտահայտության արժեքը։ Դրա համար անհրաժեշտ է հիշել գործողությունների կատարման կարգը․ սկզբում հաշվում ենք փակագծերի մեջ եղած արտահայտության արժեքը, ապա ըստ հերթականության բազմապատկում կամ բաժանումը, ապա գումարումը կամ հանումը, ընդ որում բազմապատկումը կամ բաժանումը և գումարումը կամ հանումը կատարում ենք այն հերթականությամբ, որով հանդիպում է։

Առաջադրանքներ

1. Գրի՛ր թվային արտահայտությունը և հաշվի՛ր արժեքը․

ա) (−2) և 3 թվերի արտադրյալը,
(-2)x3=-6
բ) 12 թվի կրկնապատիկը,
12×2=24
գ) 35 և 4 թվերի քանորդը,
35:4 = 8 3\4
դ) 5 թվի եռապատիկը,
5×3=15
ե) 2 և 3 թվերի գումարի կրկնապատիկը,
2+3=5 5×2=10
զ) −5 և 4 թվերի արտադրյալը,
-5×4=-20
է) 7 և 2 թվերի արտադրյալի կրկնապատիկը,
7×2=14 14×2=28
ը) 4 թվի և 6 թվի կրկնապատիկի արտադրյալը։
(4×2)x (2×6)= 96

2. Հաշվի՛ր նշված թվերի կիսագումարը․
ա) (6+24):2=15
բ) (13+49):2= 31
գ) (91+ 33):2=62
դ) (101+ 9)=55

3. Հաշվի՛ր արտահայտության արժեքը․

1. Գրատախտակին գրված են մի քանի իրարից տարբեր բնական թվեր: Դրանցից երկու ամենափոքր թվերի արտադրյալը 16 է, իսկ երկու ամենամեծ թվերի արտադրյալը՝ 225: Որքա՞ն է բոլոր թվերի գումարը:
   2+8+9+25= 44
2. Գտիր ամենամեծ թիվը, որը կարող ենք ստանալ քարտերն իրար կողք դնելով․
   
   
   309
3. Լուսինեն և Լիլիթը պայմանավորվել են հանդիպել թատրոնի մոտ ժամը 21:00-ին: Լուսինեի ժամացույցը սխալ է, այն ետ է ընկնում 3 րոպեով, սակայն նա մտածում է, որ ժամացույցն առաջ է 2 րոպե: Լիլիթի ժամացույցը նույնպես սխալ է: Այն առաջ է ընկնում 2 րոպեով, իսկ Լիլիթը մտածում է, որ այն ետ է 3 րոպե:Նրանցից ո՞վ կուշանա հանդիպումից:
   
4. Դասարանի 31 աշակերտներից 21-ը ցանկություն հայտնեց սովորել անգլերեն, իսկ  18-ը՝ ֆրանսերեն։ Քանի՞ աշակերտ ցանկություն հայտնեց սովորել երկու լեզուներն էլ։
   ոչվոք:
5. Վաճառողին հարցրին, թե քանի՞ գլուխ պանիր է այսօր վաճառել: Նա պատասխանեց. «Այսօր չորս գնորդ է եկել, նրանցից յուրաքանչյուրը գնել է մնացած պանրի կեսը և ևս կես գլուխ պանիր»: Արդյունքում ամբողջ պանիրը վաճառված է: Քանի՞ գլուխ պանիր է վաճառվել։
   4
6. Դասարանում կա 20 աշակերտ: Նրանք նստած են զույգերով: Տղաների մեկ երրորդ մասի կողքին նստած է աղջիկ, աղջիկների կեսի կողքին նստած է տղա: Քանի՞ տղա կա դասարանում:
7. Միջազգային համաժողովի 15 մասնակիցներից  10-ը խոսում էին անգլերեն, իսկ  8-ը՝  և՛ անգլերերն, և՛ ֆրանսերեն։ Հայտնի է նաև, որ 3 մասնակից այդ երկու լեզուներից ոչ մեկին չէր տիրապետում։ Քանի՞ մասնակից էր խոսում ֆրանսերեն։
   8
8. Դասարանի աշակերտներից 25-ը ցանկություն հայտնեցին սովորելու անգլերեն, 13-ը՝ գերմաներեն, 10-ը՝ ֆրանսերեն։ Միաժամանակ 7 աշակերտ ցանկություն հայտնեց սովորել անգլերեն և գերմաներեն, 4 աշակերտ՝ անգլերեն և ֆրանսերեն, իսկ գերմաներեն և ֆրանսերեն ոչ մի աշակերտ չցանկացավ սովորել։ Քանի՞ աշակերտ կար դասարանում։
   52

1.  a-ի և b-ի ի՞նչ արժեքների դեպքում կստացվի հավասարություն.
   ա) 0 : -8= 0, գ) -9 : -3 = a, ե) (–4) : 4 = –1,
   բ) 8 : 8 = 1, դ) -6: 1 = –a, զ) 3 : (–3) = –1:

2. Հայտնի են բաժանման հետևյալ հատկությունները.
(a + b) : c = a : c + b : c, (a · b) : c = (a : c) · b:
Ստուգե՛ք, որ այս հարաբերակցությունները ճիշտ են հետևյալ ամբողջ թվերի համար.
ա) a = 20, b = 10, c = –5,
բ) a = –18, b = –9, c = 3:

3. Ի՞նչ թիվ պետք է գրել աստղանիշի փոխարեն, որպեսզի ստացվի  հավասարություն.

* ։ 3 = –7, 

բ) * ։ (–8) = –6:

գ) (–*) ։ (–20) = 4,

դ) * ։ (–5) = 2:

ե) (–*) ։ 5 = –3, 

զ) (–*) ։ (–6) = 5։

4. Որո՞նք են այն չորս հաջորդական ամբողջ թվերը, որոնցից ամենամեծը հավասար է՝ ա) –11-ի, բ) 0-ի, գ) +2-ի, դ) –1-ի։

Առաջադրանքեր

1. Կատարե՛ք գումարում.
ա) (+27) + (+33)=+60
բ) (-14) + (+12)=-2
գ) (–21) + (–12)=-33
դ) (–8) + (+23)=13
ե) (–17) + (+4)=-13
զ) (–9) + (–51)=60

2. Գումարե՛ք հետեւյալ թվերը.
ա)( –10)+ (+7) +( –3) =-6
բ) (+7) +(+3) +( –4)= +6
գ) (+23)+( –40) +( +6)=-11
դ)( –18)+ (+11) +( –10)=-17
ե) (+18)+( –27) +( –5)=-14
զ)( –29)+ (+40) + (+30)=+41

3. Կատարե՛ք գումարում.
ա) (+3) + (–4)=-1 դ) (+15) + (–6)= +9, է) (–18) + (+7),
բ) (–11) + (+5)=-6, ե) (–8) + (+7)=-1, ը) (–21) + (+8)=-13,
գ) (–10) + (+3)=-7, զ) (+31) + (–10)=-21, թ) (+19) + (–12)=։

4. Խնդիրներ ֆլեշմոբից
Քառակուսու պարագիծը 52 սմ է: Գտեք այն եռանկյան պարագիծը, որի բոլոր կողմերը հավասար են և հավասար են այդ քառակուսու կողմին:

Առաջադրանքեր

1․ Կատարե՛ք գումարում.
ա) (+7) + (+2), = +9
բ) (–18) + (–3), -21
գ) (–21) + (–4),  -25
դ) (–29) + (–41)։ -70

2․ Մի հույն ծնվել է մ. թ. ա. 48 թ. եւ վախճանվել է մ. թ. 25 թ.։ Քանի՞ տարի է ապրել այդ հույնը։

3․Կատարե՛ք գումարում.
ա) (+10) + (+15), +25
բ) (–17) + (–12), -29
գ) (–45) + (–4), -50
դ) (–2) + (–9), -11
ե) (–8) + (–11)։ -19

4. Ի՞նչ թիվ պետք է գրել աստղանիշի փոխարեն, որպեսզի ստացվի հավասարություն.
ա) (-3)+ (- 8) = –11,       դ) (-2) + (-7) = –9,          է) (-5) + (-8 )= -13,
բ) –3 + -3= –6,            ե) (-6) + (-4) = –10,        ը) -14 + * = -20,
գ) –8 + -2 = –10,          զ) 7 + 2 = 9,               թ) –6 + -11= –17։

5. Թիվը ներկայացրե՛ք երկու բացասական գումարելիների գումարի տեսքով.
ա) –30, բ) –25, գ) –62, դ) –50, ե) –38։

6. Կատարե՛ք գումարում.
ա) (-3) + (–4) + (-15) + (–6)+(–18) + (-7)=-53

բ) (–11) + (-5) + (–8) + (-7) + (–21) + (-8)=-60

գ) (–10) + (-3) + (-31) + (–10) + (19) + (–12)։-85

1․ Որո՞նք  են ամենամեծ եւ ամենափոքր երկնիշ բացասական ամբողջ թվերը։

Ամենմեծ բացասակն երկնիշ թիվ -99

ամենափոքր բացասական երկնիշ թիվ -10

2․ Գրե՛ք  ստորև  բերված նախադասությունները՝ օգտագործելով + և – նշանները.

-80

+20

ա) Գիշերը  օդի ջերմաստիճանը  եղել է զրոյից 80 ցածր, իսկ ցերեկը՝ զրոյից 20 բարձր։

-80

+20
բ) Մակընթացության ժամանակ ջրի մակարդակը եղել է 0 նշագծից  315մ-ով բարձր, իսկ տեղատվության ժամանակ՝ 2110մ-ով ցածր։
գ) Մեխիկո քաղաքը գտնվում է ծովի մակերեւույթից 2240 մ բարձրության վրա, իսկ Աստրախան քաղաքը՝ ծովի մակերեւույթից 25մ ցածր։

3․Մեքենայի բաքի 7/14-ը լցնելու համար պահանջվում է 50 վայրկյան: Բաքի ո՞ր մասը կլցվի 1 րոպեում:

4. Գոյություն ունե՞ն արդյոք ամենափոքր բացասական եւ ամենամեծ դրական թվեր։

ամենամեծ դրական թվեր գոյություն չունեն

իսկ ամենամեծ բացասակն -1

5. Գրե՛ք այն երեք  հաջորդական ամբողջ թվերը, որոնցից՝
ա) ամենափոքրը –7-ն է, բ) ամենամեծը –5-ն է։

-6

• Տրված թիվը բաժանում են 7-ի, որի արդյունքում բնական թիվ չեն ստանում: Գտիր, թե 7-ի բաժանելիս ի՞նչ թվեր կարող են մնալ մնացորդում:
  1,2,3,4,5,6
• Գտիր բաժանելին, եթե բաժանարարը հավասար է 12-ի, թերի քանորդը՝ 8-ի, իսկ մնացորդը՝ 5-ի:
  101
• Ավտոբուսն ունի 36 նստատեղ: Քանի՞ ավտոբուս է պետք 370 մարդ տեղափոխելու համար:
  11
• Ավտոբուսն ունի 36 նստատեղ: Քանի՞ ավտոբուս է պետք 370 մարդ տեղափոխելու համար:
• Արդյո՞ք գոյություն ունի թիվ, որը 30-ի բաժանելիս, մնացորդում տալիս է 31:
  ոչ
• Գրիր 32:4 բաժանման տարրերը` բաժանելի, բաժանարար, քանորդ, մնացորդ:
  8 (0)
• Հաշվիր.
  ա. 168:18=9(2)
  բ.  100:14=7(2)
  գ.  285:40=7(5)
  դ.  374:24=15(14)
• Վաճառողը կշռում էր հաճախորդի գնած ապրանքը: Նա կշեռքի նժարին դրեց 10 հատ 160 գրամանոց կշռաքար, սակայն կշեռքը չհավասարակշռվեց: Ապա նա դրեց ևս մեկ 20 գրամանոց կշռաքար և կշեռքը հավասարակշռվեց:Որքա՞ն էր ապրանքի կշիռը:
  1620գ

Առաջադրանքներ

1. Աստղանիշը թվով փոխարինելով՝ ստացիր ճիշտ հավասարություն:
   ա)20 +67=88;
   բ)  37 x 14 = 518;
   գ) 451- 169 = 182;
   դ) 798 : 19 = 42:
2. Քանի՞ թվանշան է պետք 1-ից մինչև 30-ը գրելու համար
   42
3. Գործողությունները չկատարելով՝ համեմատեք արտահայտության արժեքները.
   ա) 98765+479 >     98765 + 478;
   բ) 98765 -478  >    98765 — 479;
   գ) 12345 x 987   >   12345 x 986;
   դ)  989799:31   <   989799:29:
4. Համեմատի՛ր
   ա) Արագած լեռան և Մասիսի բարձրությունները;
   բ)  Լույսի և ձայնի արագությունները;
   գ)  Մարս մոլորակի և Լուսնի հեռավորությունը երկրից;
   դ)  Միլիարդ և Գուգլ թվերը;
   ե)  Ագռավ    և  բու թռչունների կյանքի տևողությունը;
   զ)  Հայաստանում ծիրանի և բանանի ծառերի քանակը:
5. Աստղանիշը թվով փոխարինելով՝ ստացիր ճիշտ հավասարություն:
   ա) 73+ 37=99;
   բ)  57 x 17 = 969;
   գ) 352- 176 = 176;
   դ) : 35 = 137
   ե) (18+14)+30=62;
   զ) 13x (10+*)=221:
6. Գործողությունները չկատարելով՝ համեմատիր արտահայտության արժեքները.
   ա) 56789+289<56789+299;
   բ) 56789-299 <   56789-289;
   գ) 12346 x 987   >    12345 x 986;
   դ)  899868:31 <  899899:29:
7. Քանի՞ թվանշան է պետք 1-ից մինչև 450-ը գրելու համար:
   
   Լրացուցիչ առաջադրանքներ

8. Քանի՞ թվանշան է գրվում փողոցի 165 տունը համարակալելիս:
9. Գտի՛ր ամենափոքր բնական թիվը, որի թվանշանների արտադրյալը հավասար է.
   ա) 21;     բ) 216    գ) 42;     դ)36:
10.  6 ձկնորսը 6 օրում կերան 6 ձուկ: Քանի՞ օրում 10 ձկնորսը կուտեն 10 ձուկ: