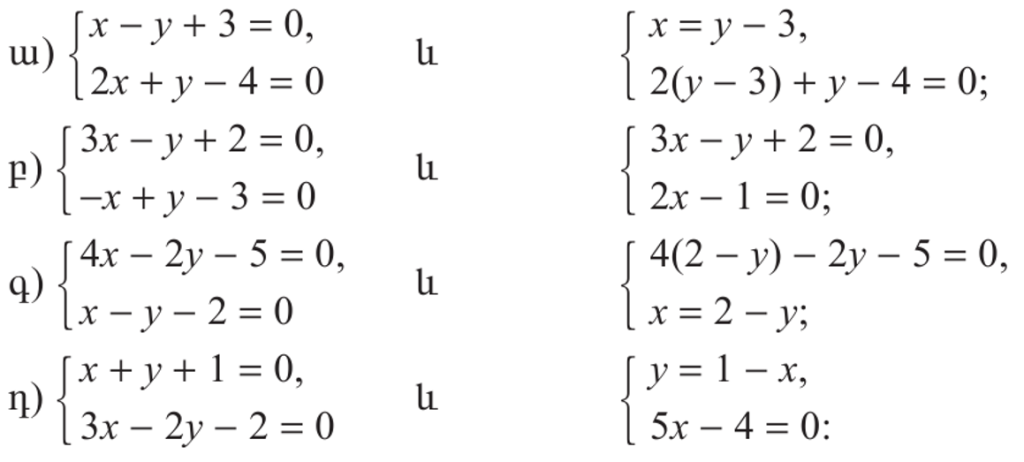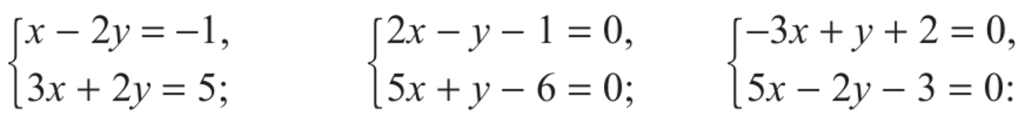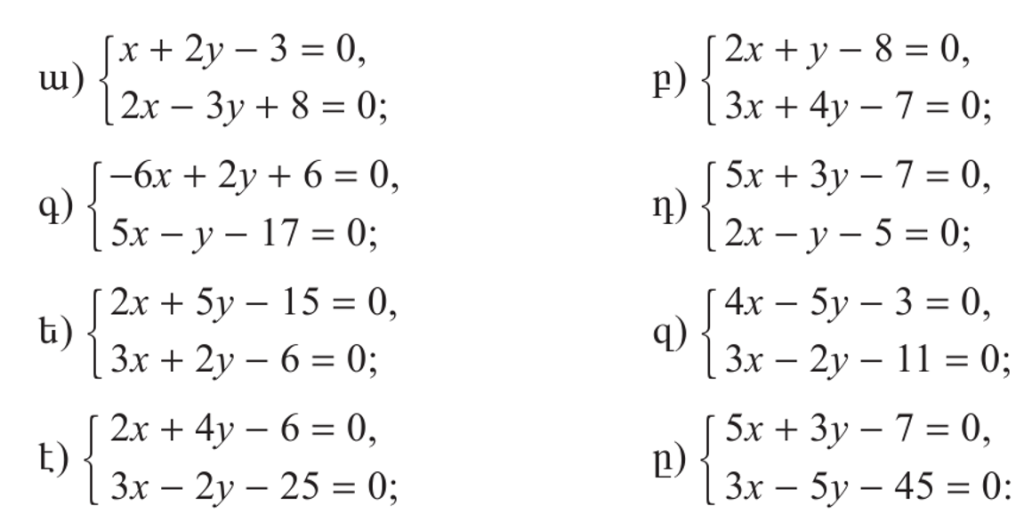Рубрика: Հանրահաշիվ

Լրացուցիչ առաջադրանքներ (տնային)

• Խնդիրները լուծի՛ր՝ անպայման համակարգ կազմելով.

1. Երկու թվերի գումարը 428 է: Եթե գումարելիներից մեկը փոքրացնենք 4 անգամ, ապա գումարը կդառնա 218: Գտի՛ր այդ թվերը:
   x+y=428
   x/4+y=218
   x+4y=872
   x=872-4y
   872-4y+y=428
   3y=444
   y=148
   x-148=428
   x=428-148=280
   Պատ․՝ 148, 280։
2. Երկու թվերի գումարը 46 է, իսկ տարբերությունը՝ 12: Գտի՛ր այթ թվերը:
   x+y=46
   x-y=12
   2x=58
   x=29
   Պատ․՝ 58, 29։
3. Երկու թվերի գումարը 84 է: Գտի՛ր այդ թվերը, եթե նրանք հարաբերում են ինչպես 3:4:
   3x-7x=84
   3x+4x=7x
   7x=84
   x=12
   x=36
   x2=12*4=48
4. Երկու թվերից մեկը 3 անգամ մեծ է մյուսից: Գտի՛ր այդ թվերը, եթե նրանց տարբերությունը հավասար է 38:
   
5. Երկու թվերից մեկը 4 անգամ փոքր է մյուսից: Գտի՛ր այդ թվերը, եթե նրանց գումարը 115 է:
6. Երկու թվերի տարբերությունը հավասար է 27: Գտի՛ր այդ թվերը, եթե նրանք հարաբերում են ինչպես 4:7:
7. Երկու թվերի գումարը 35 է, իսկ առաջին թվի կրկնապատիկի և երկրորդ թվի եռապատիկի գումարը՝ 92: Գտի՛ր այդ թվերը:

Հավելյալ առաջադրանքներ

Խնդիրները լուծի՛ր կազմելով համեմատություն.

8. 500 կգ հանքաքարից ստացել են 77 կգ պղինձ։ Ինչքա՞ն պղինձ կստացվի 300 կգ հանքաքարից։
500 * x = 77 * 300
x = 77 * 300/500
x = 46,2
Պատ.՝ 46,2 կգ
9. 160 գ ծովի ջրում պարունակվում է 8 գ աղ։ Քանի՞ գրամ ծովի ջուրն է պարունակում 56 գ աղ։
8 * x = 160 * 56
x = 160 * 56/8
x = 1120
Պատ.՝ 1120 գ
10. Բանվորը 8 ժ աշխատելու համար ստանում է 2500 դրամ։ Քանի՞ դրամ կստանա բանվորը 12 ժ աշխատելու համար։
8 * x = 12 * 2500
x = 12 * 2500/8
x = 2750
Պատ.՝ 2750 դր
11. 15 բանվորներ կատարել են աշխատանքը 24 օրում: Քանի՞ օրում այդ նույն աշխատանքը կկատարեին 18 բանվորներ:
24*15=360
360/18=20
Պատ.՝ 20։

12. Մի տակառում կա 500 լ խաղողի հյութ, իսկ մյուսում՝ 10 %-ով ավելի։ Քանի՞ լիտր խաղողի հյութ կա երկրորդ տակառում։
500 x 10/100= 5000
5000 : 100= 50
50 + 500=550
Պատ.՝ 550 լ։

13. Ո՞րն է ավելի շատ՝ 900-ի 15 %-ը, թե՞ 800-ի 20 %-ը։
900 x 15/100= 13500
13500: 100= 135
800 x 20/100= 160
160: 100= 16
135 > 16
Պատ.՝ 900-ի 15%-ը

Առաջադրանքներ(դասարանում)

1) ա) Երկու թվերի գումարը 10 է, իսկ տարբերությունը՝ 4: Գտեք այդ թվերը:
x+y=10
x-y=4
2x=14
x=7
10-7=3
Պատ․՝ (7, 3)

բ) Երկու թվերի գումարը 21 է, իսկ տարբերությունը՝ 9: Գտեք այդ թվերը:
x+y=21
x-y=9
2x=30
x=15
y=6

2) Մի թիվը 2 անգամ մեծ է մյուսից: Եթե այդ թվերից փոքրը մեծացվի 4 անգամ, իսկ մեծը՝ 2 անգամ, ապա նրանց գումարը հավասար կլինի 44: Գտեք այդ թվերը:
x=2y
2x+4y=44
x+2y=22
4x+4x=44
8x=44; x=5,5
2*5,5=11
y=11
3) Մի բնակավայրից մյուսը կարելի է գնալ գյուղամիջյան ճանապարհով կամ մայրուղով: Գյուղամիջյան ճանապարհը 5 կմ-ով կարճ է մայրուղուց, իսկ ընդհանուր երկարությունը 61 կմ է: Որքա՞ն է գյուղամիջյան ճանապարհի երկարությունը:
x = y+5
x+y = 61
y+5+y = 61
2y+5 = 61
2y = 61-5
2y = 56
y = 56/2
y = 28
x = 28+5
x = 33

Լրացուցիչ(տանը)

4) ա) Մի թիվը 6-ով մեծ է մյուսից: Այդ թվերի գումարը հավասար է 40-ի: Գտեք այդ թվերը:
x = y+6
x+y = 40
y+6+y = 40
2y+6 = 40
2y = 34
2y = 37/2
2y = 17
y = 17/2
y = 8.5
x = 8.5+6
x = 14.5

բ) Մի թիվը 15-ով փոքր է մյուսից: Գտեք այդ թվերը, եթե նրանց գումարը 23 է:
x=y+15 
x+y = 23
y+15+y = 23
2y+15 = 23
2y = 23-15
2y = 8
y = 8/2
y = 4:
x = 4+15
x = 19

5) Մի թիվը 7-ով մեծ է մյուսից: Եթե փոքր թիվը մեծացվի 2 անգամ, իսկ մեծը՝ 6 անգամ, ապա նրանց գումարը կդառնա 31: Գտեք այդ թվերը:
x=7y
2y+6x=31

6) Մի հերթափոխում նոր խառատային հաստոցով 30 դետալ ավելի է մշակվում, քան հին հաստոցով: Ընդ որում մի հերթափոխում հինգ նոր հաստոցներով կարելի է մշակել այնքան դետալ, որքան ութ հին հաստոցներով: Որքա՞ն դետալ է մշակվում նոր հաստոցով:
x=y+30
5x=8y
5y+150=8y
150=3y; y=50
x=80
Հավելյալ խնդիրներ

7) Դպրոցականները էքսկուրսիա գնացին: Նրանք վերադարձան այլ ճանապարհով, որ 7 կմ-ով կարճ էր առաջինից: Որքա՞ն է յուրաքանչյուր ճանապարհի երկարությունը, եթե դպրոցականներն ընդամենը անցան 41 կմ:
x-y=7
x+x-7=41
2x-7=41
2x=48
x=24
y=24-7=17

8) Դպրոցը ձեռք բերեց 4 բազկաթոռ և 2 սեղան, դրանց համար վճարելով 36 000 դրամ: Եթե գնվեր 2 բազկաթոռ և 3 սեղան, ամբողջ գնումը 14 000 դրամ-ով պակաս կլիներ: Առանձին-առանձին որքա՞ն  արժեն բազկաթոռը և սեղանը:

9) Երկնիշ թիվը 5 անգամ մեծ է իր թվանշանների գումարից: Եթե այդ թիվը մեծացվի 9-ով, ապա կստացվի թիվ, որը 6 անգամ մեծ է սկզբնական երկնիշ թվի թվանշանների գումարից: Գտեք երկնիշ թիվը:

Առաջադրանքներ(դասարանում)

1) Ապացուցեք, որ հավասարումները համարժեք են.

ա) 2x-3y+y=4x-2 և x+y=1;
x+y-1=0
2x-3y+y-4x+2=0
-2x-2x+2=0
x+y-1=0
Համարժեք են

բ) 5(x+y)+1=x+3 և 4x+5y-2=0:
5x+5y+1-x+3=0
4x+5y+1-3=0
4x+5y-2=0
համարժեք են

2) Կազմեք տված հավասարմանը համարժեք հավասարում.

ա) 4x-2+y=0
4x+y-2=0
4x=-y+2
16x+4y-8=0
60x-30+15y=0

բ) 5x+4y-2=2x-3y+5;
5x+4y-2-2x-3y+5=0

գ) 3x+6y-9=0;
3x-y+6-9=0

դ) x-y-1=0:
x=y-1=0

3) Համարժեք են արդյո՞ք հավասարումների համակարգերը.

Լրացուցիչ (տանը)

4) Կազմեք տված համակարգին համարժեք համակարգ.

5) Ինչպիսի՞ a-ի դեպքում հավասարումների համակարգերը համարժեք են

6) Համարժե՞ք են արդյոք հավասարումների համակարգերը.

7) Լուծեք հավասարումների համակարգը.

2500 տարի առաջ մաթեմատիկոս Պյութագորասը ստեղծեց երաժշտական գործիք՝ մոնոխորդ։ Փայտե արկղ, վրան՝ մեկ լար։ Սրա միջոցով Պյութագորասը բացահայտեց ինտերվալները։ Երաժշտական գործիքների առաջնեկն ստեղծվեց մաթեմատիկական հաշվարկների արդյունքում։

Մաթեմատիկան ամենուր է․ ձայնը չափելի է, թիվը՝ լսելի, ռացիոնալի ու էմոցիոնալի սահմանները՝ ձուլված։ Որտե՞ղ են հատվում մաթեմատիկան ու երաժշտությունը․

«Այն, որ մենք այսօր ուզում ենք կապ գտնել մաթեմատիկայի և երաժշտության մեջ, արդեն խոսում է այն մասին, որ մենք մոռացել ենք մեր սկզբնական գիտելիքը։ Ժամանակին մաթեմատիկան և երաժշտությունը չեն էլ առանձնացվել»։

Կոմիտասի անվան պետական կոնսերվատորիայում 16 տարի երաժշտության պատմության դասավանդող, երաժշտագետ, սոլֆեջիոյի մասնագետ Լիլիթ Մարտիրոսյանի սեղանին Ալեքսանդր Վոլոշոնովի հաստափոր գիրքն է՝ «Մաթեմատիկա և արվետ», դրանում մի մեծ բաժին՝ թվերով ու բանաձևերով՝ վերնագրված «Մաթեմատիկա և երաժշտություն»։ Լիլիթ Մարտիրոսյանը ցույց է տալիս գիրքն ու ասում՝  ի սկզբանե այս երկուսը չեն էլ առանձնացել՝ թվաբանությունն ու երաժշտությունը դասակարգվել են մի խմբում, երկրաչափությունն ու աստղաբաշխությունը՝ մեկ այլ։

Ավելի ուշ Դավիթ Անհաղթը մեկ այլ բաժանում է առաջարկել, որի հետ այսօր համաձայն է նաև զրուցակիցս․ այս մոտեցումն առաջարկում է հետևյալ դասակարգումը՝ թվաբանություն, երկրաչափություն, աստղաբաշխություն, այնուհետև՝ երաժշտություն։ Բացատրում է երաժշտագետը․

«Թվաբանությունն ուսումնասիրում է թվային արժեքներն ու դրանց փոխհարաբերությունները։ Երկրաչափությունն ուսումնասիրում է թվային արժեքները որոշակի դասավորվածության մեջ՝ հարթության վրա կամ տարածության մեջ, և այդ դասավորվածության պայմանում նրանց փոխհարաբերությունները։ Հաջորդը ատղաբաշխությունն է, որտեղ տարածության մեջ դասավորված թվային արժեքները նաև շարժվում են։ Երաժշտության պարագայում այս բոլոր կետերին ավելանում է ևս մեկը՝ հնչողությունը»։

7 նոտա, դրանք գրելու համար՝ 5 գիծ, ինտերվալը ներկայացնելու համար՝ մաթեմատիկական–երաժշտական անուններ՝ 1-ը՝ պրիմա, 2-ը՝ սեկունդա, 3-ը՝ տերիա, այնուհետև՝ կվարտա, կվինտա, սեկստա, սեպտիմա, օկտավա և այլն։

Տատանումների հաճախականություն, հնչյունների փոխհարաբերություն, դրանց միջև տարածություն..․ երաժշտությունը «կարդալիս» թիվ տեսնելու համար մեծ ջանքեր հարկավոր չեն։

«Երաժշտությունը՝ հանրահաշվական վարժություն է հոգու համար, այն հաշվարկ Է կատարում  չգիտակցելով դա»

Գոթֆրիդ Լայբնից

Հանրահաշիվը երաժշտության ներքո 

Գիտնականներին վաղուց հետաքրքրում էր. թե ինչու՞ երաժշտության մեջ օկտավան բաղկացած է յոթ հիմնական ձայներից, այնքան որքան գույն կա արևի լույսի լուսապատկերում: Դեռ ոչինչ չիմանալով բնության ձայների մասին, մարդը բնազդաբար դասավորել է լարերն այնպես, որ նրանք բարեհունչ հնչեն:

• Պյութագորասին է պատկանում հարմոնիայի հիմունքների մաթեմատիկական բացատրությունը: Պյութագորասի սահմանմամբ, մարդկանց կողմից էլ ավելի բնական է ընկալվում այն հաճախությունները,որոնք գտնվում են պարզ թվային հարաբերությունների միջև: Ահա որտեղից է օկտավաներում հաճախության հարաբերակցությունը 1:2 և ներդաշնակ հաճախությունների  հարաբերակցությունը  4:5:6: Հաջորդաբար կրճատելով լարերի երկարությունները կստանանք 16 հնչյունից բաղկացած բնական ձայների հնչյունաշարը:

Առաջադրանքներ(դասարանում)

1) Լուծեք հավասարումների համակարգը գործակիցների հավասարեցման (գումարման մեթոդով).

Լրացուցիչ (տանը)

2) Լուծեք հավասարումների համակարգը գործակիցների հավասարեցման (գումարման մեթոդով).

3) Հավասարումների համակարգը լուծել տեղադրման և գումարման եղանակներով.

1. Աղջիկների մի խումբ շրջան է կազմել: Գայանեն Անահիտից հետո չորրորդն է ձախից և յոթերորդը՝ աջից: Քանի՞ աղջիկ է շրջան կազմել:
7+4-2=9

2. Նկարում պատկերված է յոթ հավասարակողմ եռանկյուն: Կետագծի երկարությունը 20 է: Որքա՞ն է սև գծի երկարությունը:
2*20=40
Պատ․՝ 40

3. 186 թիվը ներկայացրեք երեք այնպիսի գումարելիների գումարի տեսքով, որոնցից յուրաքանչյուր երկուսի գումարը բաժանվում է երրորդի վրա։Նշիր այդ թվերից մեծագույնը:
186:6=31
31*3=93
31*2=62
Պատ․՝93
4.  Մենք ունենք 10 փակ կողպեք և դրանք բացող 10 բանալի, որոնք խառնվել են։ Ամենաքիչը քանի՞ փորձից հնարավոր կլինի բոլոր փակ կողպեքները բացել այդ 10 բանալիով:
10

5. Լուծի՛ր համակարգերը տեղադրման մեթոդով.

6. Երկու գումարելիներից մեկը 1005 է, իսկ մյուսը՝ նրա 11/3-­ը։ Ինչի՞ է հավասար գումարը։
11/3=3 2/3 = 1005 * 3 2/3= 3350
1005+3350=4355

7. Բերված պնդումներից որո՞նք են ճիշտ, որո՞նք՝ սխալ.

ա) Երկու զույգ թվերի գումարը զույգ թիվ է։

բ) Երկու կենտ թվերի գումարը զույգ թիվ է։

գ) Եթե երկու բնական թվերի արտադրյալը բաժանվում է 4­ի, ապա արտադրիչներից գոնե մեկը բաժանվում է 4­ի։

դ) Որպեսզի բնական թիվը բաժանվի 5­ի, անհրաժեշտ է, որ նրա գրառումն ավարտվի
5-­ով։

ե) Եռանկյան ցանկացած երկու կողմերի երկարությունների գումարը երրորդ կողմի երկարությունից մեծ է։

Հավելյալ խնդիրներ

8. 15 սմ կողմով քառակուսի հախճասալիկները փոխարինում են նորերով, որոնց կողմի երկարությունը 20 սմ է։ Քանի՞ նոր հախճա­սալիկ է պետք 80 հների փոխարեն։
80 * 15 = 1200
1200 : 20 = 60                                      
Պատ.՝ 60 նոր հախճասալիկ

9. Մեքենան ճանապարհի վերջնակետին է հասել 2 օրում։ Առաջին օրն այն անցել է 450 կմ, երկրորդ օրը՝ առաջին օրն անցածի 43­ը։ Յուրաքանչյուր 100 կմ ճանապարհն անցնելու համար մեքենան ծախսել է 11 լ բենզին։ Քանի՞ լիտր բենզին է անհրաժեշտ եղել ամբողջ ճանապարհն անցնելու համար։

 10. Երկու արհեստանոցներ 1 ամսում պիտի որոշակի քանակով ման­րակներ պատրաստեին։ Առաջին արհեստանոցը կատարեց աշխատանքի ­3/4ը, իսկ երկրորդը՝ առաջինից 3 անգամ պակաս։ Կարողացա՞ն արդյոք արհեստանոցները ժամանակին կատարել նախատեսված աշխատանքը։

11. Տուփի մեջ կան 31 կարմիր և 96 սպիտակ գնդիկներ։ Առանց նայելու` առնվազն քանի՞ գնդիկ պետք է վերցնել տուփից, որպեսզի նրանց մեջ անպայման լինեն նույն գույնի երկու գնդիկներ։ Կփոխվի՞ արդյոք պատասխանը, եթե կարմիր և սպիտակ գնդիկների քանակները նույնը լինեն, օրինակ՝ ամեն գույնի 50 գնդիկ։

12. Լուծի՛ր համակարգերը.

Առաջադրանքներ (դասարանում)

1) Եռանկյան կողմերը հավասար են 6սմ, 8սմ, 10սմ: Գտեք այն եռանկյան պարագիծը, որի կողմերը տրված եռանկյան միջին գծեր են:
10:2=5
6:2=3
8:2=4
P=5+3+4=12
2) Ուռուցիկ քառանկյան անկյունագծերը հավասար են 12մ և 16մ: Գտեք այն քառանկյան կողմերը, որի գագաթները տրված քառանկյան կողմերի միջնակետերն են:
12:2=6
16:2=8
P=6+6+8+8=28

3) Նկարում EF||AC: Գտնել PBEF և PABC:

Լրացուցիչ առաջադրանքներ (տանը)

4) Նկարում MN || AC: Գտնել PMBN և PABC:

5) Քառանկյան անկյունագծերը հավասար են m-ի և n-ի: Գտեք այն քառանկյան պարագիծը, որի գագաթները տրված քառանկյան կողմերի միջնակետերն են:
m/2+n/2 +n/2 +m/2

6) Ապացուցեք, որ ուռուցիկ քառանկյան կողմերի միջնակետերը զուգահեռագծի գագաթներ են:

7)* Ապացուցեք, որ եռանկյան գագաթները հավասարահեռ են նրա որևէ միջին գիծն ընդգրկող ուղղից:

1. Լուծի՛ր համակարգերը տեղադրման մեթոդով.

2. Ուղղանկյան մակերեսը 900 սմ² է։ Քանի՞ քառակուսի սանտիմետր  է նրա մակերեսի 1 %-ը: Քանի՞ քառակուսի սանտիմետր է նրա մա­կերեսի 16 %-ը։
900 x 1 = 900
900 : 100 = 9
Պատ.՝ 9 սմ քառ.
900 x 16 = 14400
14400 : 100 = 144
Պատ.՝ 144 սմ քառ

3. Զամբյուղում կա 300 խնձոր։ Գտե՛ք խնձորների քանակի 20 %-ը։
300 x 20 = 6000
6000 : 100 = 60
Պատ.՝ 60

4. Մի գյուղացին իր այգուց հավաքել է 1500 կգ խաղող, իսկ մյուսը՝ 30 %-ով պակաս։ Ընդամենը քանի՞ կիլոգրամ խաղող են հավաքել երկու գյուղացիները։

5. Որքա՞ն է 536­ի 100 %­ը։
536 x 100 = 53600
53600 : 100 = 536
Պատ.՝ 536

Լրացուցիչ առաջադրանք (տանը)

6. Լուծի՛ր համակարգերը տեղադրման մեթոդով.

7. Զբոսաշրջիկն անցել է ճանապարհի ­1/4ը։ Ճանապարհի քանի՞ տո­կոսն է նա անցել։
Պատ.՝ 25%-ը

8. Մի տակառում կա 500 լ խաղողի հյութ, իսկ մյուսում՝ 10 %-ով ավելի։ Քանի՞ լիտր խաղողի հյութ կա երկրորդ տակառում։

9. Ո՞րն է ավելի շատ՝ 900-ի 15 %-ը, թե՞ 800-ի 20 %-ը։
900 x 15 = 13500
13500 : 100 = 135
800 x 20 = 16000
16000 : 100 = 160
135 <160
Պատ.՝ 800-ի 20%-ը մեծ է

Հավելյալ խնդիրներ

10. Պատասխանե՛ք հետևյալ հարցերին. 

ա) 1 մետրի քանի՞ տոկոսն է 1 դեցիմետրը.

բ) 10 տոննայի քանի՞ տոկոսն է 1 ցենտները.

գ) 1 քառակուսի մետրի քանի՞ տոկոսն է 1000 քառակուսի սանտիմետրը։

11. Ուսանողի թոշակն ավելացել է 2 անգամ։ Քանի՞ տոկոսով է ավելացել թոշակը։

Առաջադրանքներ (դասարանում)

1) Տեղադրման եղանակով լուծեք հավասարումների համակարգը.

2) Լուծեք հավասարումների համակարգը.

Լրացուցիչ առաջադրանքներ (տանը)

3) Տեղադրման եղանակով լուծեք հավասարումների համակարգը.

4) Լուծեք հավասարումների համակարգը.

Հավելյալ խնդիրներ

5) Կենդանու գլուխը կշռում է այնքան ինչքան վերջույթներն ու մարմնի կեսը, իսկ մարմինը՝ այնքան, որքան վերջույթներն ու գլուխը միասին։ Պարզվում է , որ վերջույթները կշռում են 1կգ, որքան է կենդանու ընդհանուր քաշը։

6) Գտեք օրինաչափությունը և հաջորդ թիվը լրացրեք.
1, 8, 27, 64, 125, 216, 343, 512, 729, …

7) 4000538 թվից հինգ թվանշան այնպես ջնջեք, որ մնացած թիվը լինի հնարավոր
ամենամեծը:

8) Մաթեմատիկական մրցույթի ժամանակ 20 հարց էր տրված: Յուրաքանչյուր ճիշտ
պատասխանի դեպքում թիմը 12 միավոր էր ստանում, իսկ սխալ պատասխանի
դեպքում հանում էին 10 միավոր:Քանի՞ ճիշտ պատասխան էր տվել թիմը, եթե
պատասխանել էր բոլոր հարցերին և հավաքել էր 86 միավոր:

9) Երկու թվերի գումարը 715 է: Թվերից մեկը 0-ով է վերջանում: Եթե այդ 0-ն ջնջենք, մյուս թիվը կստացվի: Գտեք այդ թվերը:

10) Արկղում 30 գնդիկ կա՝ սև և սպիտակ: Հայտնի է, որ ցանկացած 12 գնդիկից գոնե մեկը սպիտակ է, և ցանկացած քսանից գոնե մեկը՝ սև: Քանի՞ սև գնդիկ կա: