Рубрика: Երկրաչափություն

Առաջադրանքներ (դասին և տանը)

Առաջադրանքներից յուրաքանչյուրից կամ որոշ խմբերից առաջ նշված են բոլոր այն սահմանումները, որոնք անհրաժեշտ են խնդիրները լուծելու համար:

Տեսական մաս

Խնդիրներ

ABCD քառանկյունը սեղան է։

Տեսական մաս

Խնդիրներ

247. ABCD սեղանը հավասարասրուն է

Տեսական մաս

Խնդիրներ

Առաջադրանքներ (դասարանում)

1) Շեղանկյան անկյունագծերից մեկը հավասար է կողմին: Գտեք՝

ա) շեղանկյան անկյունները,
AC=AB=BC=>
=><BAC=<BCA=<B=60
<B=<D=60
<A=<C=120
Պատ․՝ 120, 60, 120, 60։
բ) այն անկյունները, որոնք կազմում են շեղանկյան անկյունագծերը նրա կողմերի հետ:

2) ABCD շեղանկյան մեջ <B=120⁰: Անկյունագծերը հատվում են O կետում: BC կողմը 10սմ է: Գտեք BD անկյուանգիծը:
360-240=120
120:2=60
60:2=30
10:2=5
BO=5
BO=OD
5+5=10
Պատ՝ 10 սմ

3) Քառակուսու անկյունագծերի հատման կետից մինչև կողմերը եղած hեռավորությունների գումարը 20սմ է: Գտեք քառակուսու պարագիծը:

4) Քառակուսու պարագիծը 80սմ է: Որքա՞ն է քառակուսու անկյուանգծի միջնակետի հեռավորությունը նրա կողմից:

Լրացուցիչ(տանը)

5) Գտեք ABCD շեղանկյան պարագիծը, եթե <B=60⁰, AC=10,5սմ:
AO=10,5:2=5,25
AB=10,5
10,5×4=42
Պատ՝ 42սմ:

6) Գտեք այն անկյունները, որոնք կազմում են շեղանկյան անկյունագծերը նրա կողմի հետ, եթե հայտնի է, որ շեղանկյան անկյուններից մեկը 45⁰ է:

7) Շեղանկյան գագաթներից մեկով նրա հանդիպակաց անկյունը կազմող կողմերին տարված ուղղահայացները կազմում են 30⁰-ի անկյուն, ընդ որում՝ դրանցից յուրաքանչյուրի երկարությունը 5 սմ է: Գտեք շեղանկյան կողմը:
5×2=10սմ
Պատ՝ 5սմ:
Հավելյալ խնդիրներ

8) Ապացուցեք, որ եթե շեղանկյան մի անկյունը ուղիղ է, ապա այդ շեղանկյունը քառակուսի է:

9) Քառակուսի՞ է արդյոք քառանկյունը, եթե նրա անկյունագծերը՝

ա) հավասար են և փոխուղղահայաց,

բ) փոխուղղահայաց են և ունեն ընդհանուր միջնակետ,

գ) հավասար են, փոխուղղահայաց են և ունեն ընդհանուր միջնակետ:

10) Ուղղանկյուն եռանկյան ուղիղ անկյան կիսորդի և ներքնաձիգի հատման կետով տարված են էջերին զուգահեռ ուղիղներ: Ապացուցեք, որ առաջացած քառանկյունը քառակուսի է:

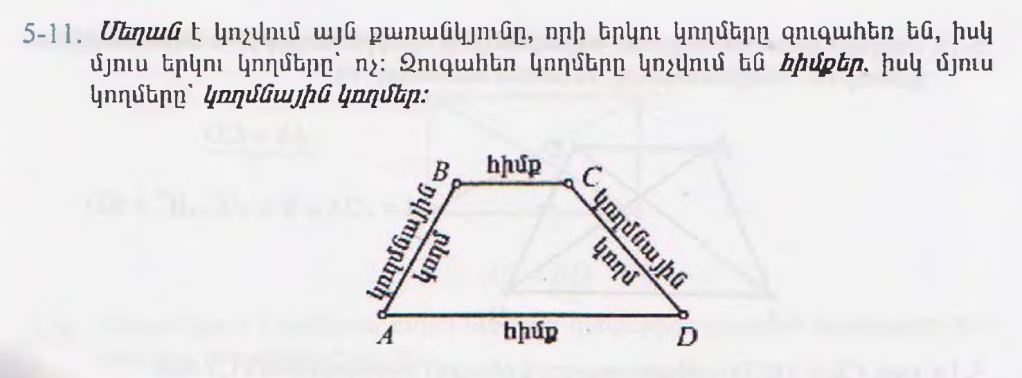
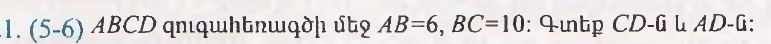Առաջադրանքներ(դասարանում)

1) ABCD ուղղանկյան անկյունագծերը հատվում են O կետում: <COD=60⁰, CD=10սմ: Գտեք ուղղանկյան անկյունագծերը:
180-60=120
120:2=60
OC=OD
<C=<D=60=>OC=AO=OD=OB=10
10+10=20
AC=BD=20

2)Գտեք ABCD ուղղանկյան պարագիծը, եթե A անկյան կիսորդը տրոհում է՝

ա) BC կողմը 45,6սմ և 7,85սմ երկարությամբ հատվածների,
7+45,6=58,45
BD=AC=53,45
<1=<2(խաչադիր անկյուններ)
90:2=45
<3=<2=45=>եռ.ABE-հավասարասրուն=>AB=CD=7,85
P=58,45+58,45+7,85+7,85=132,6

բ) DC կողմը 2,7դմ և 4,5դմ երկարությամբ հատվածների:
2.7+4.5=7.2
7,2+2,7=11,7
11,7*2=23,4
Լրացուցիչ(տանը)

3)Ապացուցեք, որ այն զուգահեռագիծը, որի անկյուններից մեկը ուղիղ է, ուղղանկյուն է:
Քանի որ զուգահեռագծի հանդիպակաց անկյունները իրար հավասար են, և կողմին առընթեր անկյունների գումարը 180 աստիճան է։

4)Ապացուցեք, որ եթե քառանկյան բոլոր անկյունները ուղիղ են, ապա քառանկյունը ուղղանկյուն է:
Քանի որ, քառանկյան բոլոր անկյունների գումարը 360աստիճան է և բոլոր անկյունները իրար հավասար են=>իրենք անպայման պետք է կազմեն 90 աստիճան, որ իրենց գումարը ստացվի 360 աստիճան:

5)Ապացուցեք, որ եթե զուգահեռագծի բոլոր անկյունները հավասար են, ապա այն ուղղանկյուն է:
Քառանկյան ներքին անկյունների գումարը 360 աստիճան է, բոլոր անկյունները իրար հավասար են, հավասար են 90 աստիճան է պատկերը ուղղանկյուն է։

6)ABCD ուղղանկյան անկյունագծերը հատվում են O կետում, E-ն AB կողմի միջնակետն է, <BAC=50⁰: Գտեք <AOE-ն:
40, 50

7) Ուղղանկյան անկյունագծերի հատման կետի հեռավորությունը մեծ կողմից 4սմ է, իսկ փոքր կողմից՝ 6սմ: Գտեք ուղղանկյան պարագիծը:
6*2=12
BC=12
4*2=8
P=12+12+8+8=40սմ

Առաջադրանքներ (դասարանում)

1) Ուղղանկյուն սեղանի մեջ սուր անկյունը 45⁰ է: Փոքր սրունքը և փոքր հիմքը 10-ական սմ են: Գտեք սեղանի մեծ հիմքը:
C գագաթից AD -ին տանենք CK ուղղահայաց, որպես AD-ի ուղղահայացներ ` AB// CK:
ABCK-ն զուգահեռագիծ է:
AB=CK=10 և BC=AK=10CKD ուղղանկյան եռանկյան մեջ <D=45
<C=45
CKD հավասարասրուն է:
KD=CK=10
AB=AK+KD=10+10=20 սմ
Պատ՝. 20 սմ

2)Ուղղանկյուն սեղանի հիմքերն են a և b, անկյուններից մեկը՝ : Գտեք՝

ա) սեղանի մեծ սրունքը, եթե a=4սմ, b=7սմ, =60⁰,
բ) սեղանի փոքր սրունքը, եթե a=10սմ, b=15սմ, =45⁰

Լրացուցիչ (տանը)

3) Սեղանի սրունքներից մեկը բաժանված է երեք հավասար հատվածների: Այդ բաժանման կետերից տարված են մյուս սրունքին միացնող հատվածներ, որոնք զուգահեռ են սեղանի հիմքերին: Գտեք այդ հատվածների երկարությունները, եթե սեղանի հիմքերը հավասար են 2 սմ և 5 սմ:
BC = 2 սմ
AD = 5 սմ
HM, NF – ?
HM = BC + NF / 2
NF = HM + AD / 2
2 + NF =2 HM
5 + HM = 2 NF
NF = 2HM – 2
5+HM =2 * (2HM – 2)
5 + HM = 4 HM – 4
9 = 3HM
HM = 3 սմ
NF = 4 սմ

4) Տրված ուղղի տարբեր կողմերում տրված են M և N կետերը, որոնց հեռավորությունները այդ ուղղից հավասար են 10սմ և 6սմ: Գտեք MN հատվածի միջնակետի հեռավորությունը տրված ուղղից:
(DN+BM) : 2 = (10 + 22) : 2 = 32 : 2 = 16սմ
CA = 16սմ

Առաջադրանքներ (դասարանում)

1) Գտեք AD և BC հիմքերով սեղանի B և D անկյունները, եթե <A=36⁰, <C=117⁰:
<B=180-36=144⁰
<D=180-117=63⁰
Պատ․՝ 144⁰, 63⁰։

2) Հավասարասրուն սեղանի մեծ հիմքը 4մ է, սրունքը՝ 2մ, իսկ դրանց կազմած անկյունը՝ 60⁰: Գտեք սեղանի փոքր հիմքը:

3) Գտեք հավասարասրուն սեղանի անկյունները, եթե հայտնի է, որ սեղանի երկու անկյունների տարբերությունը 40⁰ է:
180-40=140
140:2=70°
70°+40°=110°
Պատ․՝ 110 և 70։

Լրացուցիչ (տանը)

4) Ապացուցեք, որ հավասարասրուն սեղանի յուրաքանչյուր հիմքին առընթեր անկյունները հավասար են:

5) Սեղանի հիմքերը հարաբերում են, ինչպես 2:3, իսկ միջին գիծը 10սմ է: Գտեք սեղանի հիմքերը:
EF = BC+AD/2= 2x+3x/2=
2x+3x=20
5x=20
X=4

6) M և N կետերը գտնվում են տրված ուղղի մի կողմում, և նրանց հեռավորությունները այդ ուղղից հավասար են 10սմ և 22սմ: Գտեք MN հատվածի միջնակետի հեռավորությունը այդ ուղղից:

7) Հավասարասրուն սեղանի բութ անկյան գագաթից նրա մեծ հիմքին տարված ուղղահայցն այդ հիմքը տրոհում է 6սմ և 30սմ երկարությամբ հատվածների: Գտեք սեղանի փոքր հիմքը և միջին գիծը:

Տեսական նյութ

Թեորեմ (Թալես)Եթե երկու ուղիղներից մեկի վրա հաջորդաբար տեղադրվեն մի քանի հավասար հատվածներ և նրանց ծայրակետերով տարվեն զուգահեռ ուղիղներ, որոնք հատեն երկրորդ ուղիղը, ապա երկրորդ ուղղի վրա անջատվում են միմյանց հավասար հատվածներ:

Առաջին դեպք, երբ ուղիղները զուգահեռ են՝ l1|| l2

Երկրորդ դեպք, երբ ուղիղները զուգահեռ չեն՝ 

:

Առաջադրանքներ (դասարանում)

1) ABC եռանկյան AB և AC կողմերի վրա համապատասխանաբար նշված են M և N կետերն այնպես, որ MN || BC: Գտնել

ա) AN:AC և AN:NC, եթե AM:AB=3:7;
AN:AC=3:7
AN:NC=3:4

բ) NC-ն, եթե AM=3սմ, AB=9սմ և AN=2սմ;
9:3=3
3*2=6
6-2=4

գ) AN, եթե AM:AB=2:3 և AC=15սմ;
15:3=5
AN=2*5=10

դ) AN, եթե AM=2սմ, NC=8սմ և AN=MB: 
?

Լրացուցիչ (տանը)

2) Գրի՛ր տեղեկություններ Թալեսի և Թալեսի թեորեմի մասին:
Թալես Միլեթացի, հին հույն փիլիսոփա, մաթեմատիկոս, տոմարագետ, աստղագետ, ճարտարապետ։ Թալեսը համարվում է հունական յոթ իմաստուններից մեկը։ Արիստոտելը նրան համարում է հույն առաջին փիլիսոփան։ Ընդունված է Թալեսին պատմականորեն համարել առաջին անհատը, ով զբաղվել է գիտական փիլիսոփայությամբ։ Հաճախ նրան անվանում են գիտության հայր։ 
Ծնվել է Միլեթոս քաղաքում։ Թալեսը Միլեթյան դպրոցի առաջին փիլիսոփա-գիտնականն է, առաջին մաթեմատիկոսն ու բնագետը։ Նա եղել է իր ժամանակի ամենախոշոր մարդը, միաժամանակ զբաղվել է առևտրով, եղել է հայտնի վաճառական, քաղաքական խոշոր գործիչ, ճարտարապետ, աստղաբաշխ, ճանապարհորդել է զանազան քաղաքներ, դեպի Եգիպտոս, որտեղ զբաղվել է Նեղոսի հեղեղումների ուսումնասիրությամբ։ Վերադառնալով Միլեթոս իրեն նվիրում է գիտական զբաղմունքի մինչև խոր ծերություն։

3) ΔABC եռանկյան AB, BC և AC կողմերի վրա համապատասխանաբար վերցված L, M և N կետերն այնպես, որ LM || AC, MN || AB: Գտնել ALMN զուգահեռագծի կողմերը, եթե նրա պարագիծը18սմ, AC = 8սմ, АВ = 12սմ:

Առաջադրանքներ (դասին և տանը)

Մաթեմատիկական ֆլեշմոբ
Մասնակցել եմ

Առաջադրանքներ (դասարանում)

1) Եռանկյան կողմերը հավասար են 6սմ, 8սմ, 10սմ: Գտեք այն եռանկյան պարագիծը, որի կողմերը տրված եռանկյան միջին գծեր են:
6+8=14
14+10=24
24/2=12
Պատ․՝12

2) Ուռուցիկ քառանկյան անկյունագծերը հավասար են 12մ և 16մ: Գտեք այն քառանկյան կողմերը, որի գագաթները տրված քառանկյան կողմերի միջնակետերն են:
12:2=6
16:2=8
Պատ․՝ 6,8

3) Նկարում EF||AC: Գտնել PBEF և PABC:

Լրացուցիչ առաջադրանքներ (տանը)

4) Նկարում MN || AC: Գտնել PMBN և PABC:

5) Քառանկյան անկյունագծերը հավասար են m-ի և n-ի: Գտեք այն քառանկյան պարագիծը, որի գագաթները տրված քառանկյան կողմերի միջնակետերն են:
P=2*0.5m+2*0.5n=m+n
Պատ․՝P=m+n

6) Ապացուցեք, որ ուռուցիկ քառանկյան կողմերի միջնակետերը զուգահեռագծի գագաթներ են:

7)* Ապացուցեք, որ եռանկյան գագաթները հավասարահեռ են նրա որևէ միջին գիծն ընդգրկող ուղղից:

1) ABCD ուռուցիկ քառանկյան մեջ AB=CD, <B=70⁰, <BCA=60⁰, <ACD=50⁰: Ապացուցեք, որ BC=AD:
AB=CD,
<B=70⁰,
<BCA=60⁰,
<ACD=50⁰
Ըստ առաջին հայտանիշի
360-60-70-50=180
BC=AD

Լրացուցիչ առաջադրանքներ (տանը)

11) ABCD քառանկյան AB, BC, CD և DA կողմերի վրա նշված են համապատասխանաբար M, N, P և Q կետերն այնպես, որ AM=CP, BN=DQ, BM=DP, NC=QA: Ապացուցեք, որ ABCD-ն և MNPQ-ն զուգահեռագիծ են:

12) ABCD զուգահեռագծի BD անկյունագծի վրա P և Q կետերը նշված են այնպես, որ BP=QD: Ապացուցեք, որ APCQ քառանկյունը զուգահեռագիծ է: