Երկրաչափություն․Եռանկյունների նմանության հաշտանիշներ

Եռանկյունների նմանության առաջին հայտանիշը

I. Եթե մի եռանկյան երկու անկյունները համապատասխանաբար հավասար են մյուս եռանկյան երկու անկյուններին, ապա եռանկյունները նման են:  

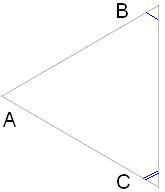
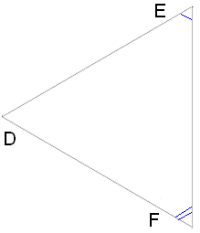
Եթե ∢B=∢E և ∢C=∢F, ապա ΔABC∼ΔDEF

Եռանկյունների նմանության երկրորդ հայտանիշը

II. Եթե մի եռանկյան երկու կողմերը համեմատական են մյուս եռանկյան երկու կողմերին, իսկ այդ կողմերով կազմված անկյունները հավասար են, ապա եռանկյունները նման են:

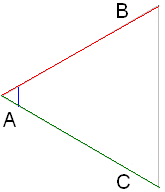
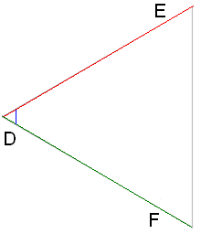
Եթե AB/DE = AC/DF և ∢A = ∢D, ապա ΔABC∼ΔDEF

Եռանկյունների նմանության երրորդ հայտանիշը

III. Եթե մի եռանկյան երեք կողմերը համեմատական են մյուս եռանկյան երեք կողմերին, ապա եռանկյունները նման են:

Եթե AB/DE = BC/EF = AC/DF, ապա ΔABC∼ΔDEF

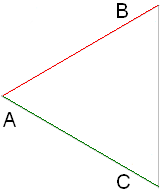
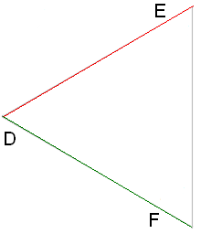
Խնդիրներ լուծելիս, սկզբում պետք է համոզվել, որ տրված եռանկյունները նման են:

Եթե եռանկյունների նմանությունը տրված չէ, ապա դա պետք է ապացուցել:

Դասարանական առաջադրանքներ՝ 171; 173; 175

Լրացուցիչ առաջադրանքներ՝ 172; 174; 176

171. 15/8 ≠ 20/6
ոչ

172. 90 – 40 = 50
ա․ այո բ․ ոչ

173. Զուգահեռ ուղիղների համապատասխան անկյունները հավասար են
∠A = ∠CPQ
∠C-ն ընդհանուր է

Հետևում է, որ եռանկյունները նման են։

174. Զուգահեռ ուղիղների համապատասխան անկյունները հավասար են
∠A = ∠BDE
∠B-ն ընդհանուր է

Հետևում է, որ ∆ABC~∆BDE

20/15 = 16/AD
4/3 = 16/AD
4AD = 48
AD = 12

175. ∆ABC~∆BDE
ա․ 20/DE = 17/11,9
17D = 238
D = 14
բ․ 15 – 10 = 5
18/DE = 15/5
18/DE = 3
3DE = 18
DE = 6